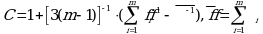Анализ достоверности данных

2.11. Важной задачей является обнаружение выбросов в наборе дисперсий, вычисленных по наборам выборочных данных, в частности как при определении точности методов измерений, так и при поиске значений, полученных в результате подбора данных, а не проведения исследований.

С целью определения значимости отличия наибольших дисперсий от остальных в исследуемом наборе используется критерий Кохрена, задаваемый формулой 4:

, где (4)

- наибольшее значение дисперсии в наборе из N дисперсий.

Вычисляется отношение максимального значения изменчивости (дисперсии) среди N опытов к сумме изменчивостей во всех N опытах. Найденное наибольшее экспериментальное значение G сравнивают с критическим его значением G_Kp Значение G_Kp представляет собой максимально возможное значение параметра G, при котором гипотеза о воспроизводимости эксперимента еще может считаться справедливой. В этом случае максимальная изменчивость функции отклика, полученная в результате проведения n параллельных опытов, не отличается от ожидаемой среди N опытов. Поэтому если G <= G_Kp, то "подозрительное" максимальное значение изменчивости не является "инородным", а представляет собой результат случайного рассеяния исследуемой функции отклика, т.е. эксперимент воспроизводим.

В противном случае (когда G > G_Kp) эксперимент не воспроизводим, и необходимо повторить его в анализируемой экспериментальной точке, добившись воспроизводимости, т.е. выполнения G_Kp >= G.

2.12. В том случае, если объемы выборок (количество проведенных исследований) по каким-либо причинам различны или имеет место предположение об отличии наименьшей дисперсии из представленных (что может быть вызвано подбором экспериментальных данных), то с целью проверки отклонения дисперсий необходимо воспользоваться критерием Бартлетта.

Нулевая гипотеза (об однородности дисперсий) для данного критерия формулируется следующим образом:

Для ее проверки необходимо определить средневзвешенную дисперсию, которая задается формулой 5:

, где (5)

f_i = n_i - 1 число степеней свободы выборки; m - число сравниваемых дисперсий.

Случайная величина B задается формулой 6:

, где (6)

Бартлеттом было показано, что случайная величина B распределена приближенно как с числом степеней свободы, равным m - 1, если все fi > 2, т.е. объем каждой из выборок должен быть не менее 4. Критическую область строят правостороннюю исходя из требования, чтобы вероятность попадания B-критерия в нее в предположении справедливости нулевой гипотезы была равна принятому уровню значимости:

Критическую точку находят по таблицам процентных точек - распределение для уровня значимости и числа степеней свободы f = m - 1. Если, нуль-гипотезу отвергают. Следует отметить, что критерий Бартлетта весьма чувствителен к отклонениям сравниваемых распределений от нормального, поэтому при получении сомнительных результатов необходимо дополнительно проводить проверку на нормальность распределения исследуемых показателей.

Пример. Четырьмя лабораториями была измерена концентрация вещества в пищевом продукте. Дисперсии и объемы выборок приведены в табл. 1.

Таблица 1

Дисперсии и объемы выборок результатов измерения

концентраций вещества в пищевом продукте

Требуется проверить гипотезу об однородности дисперсий при условии, что выборки распределены по нормальному закону. Число степеней свободы B-критерия равно f = 4 - 1 = 3. Поскольку рассчитанное значение критерия Бартлетта меньше табличного для уровня значимости 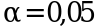и числа степеней свободы f = 3, следовательно сравниваемые выборки принадлежат одной генеральной совокупности, т.е. однородны:

2.13. В пунктах 2.14 - 3.33.8 представлены алгоритмы анализа для автоматизации оценки достоверности результатов исследований с целью получения корректной статистической информации.

2.14. Оценка достоверности проведения исследования по показателям, участвующим в расчете калорийности. Суммируются числовые значения в ячейках по одной строке (для одного продукта) (в разделе "Исследования"): "Содержание жира, г/100 г" + "Содержание белка, г/100 г" + "Содержание золы, %" + "Влажность, %" + "Углеводы (расчетные), г/100 г" + "Пищевые волокна, %" = значение. Полученные значения записываются во вновь созданный столбец "Сумма пищевых веществ аналитическая, на 100 г".

Те образцы, которые оказались вне эталонного диапазона для данного показателя , должны быть помечены любым способом и отправлены оператору ввода данных на доработку.

2.15. Оценка достоверности исследования показателя "Жирнокислотный состав". Алгоритм применим для тех групп продуктов, где определялся показатель "Жирнокислотный состав". Суммируются числовые значения в следующих ячейках по одной строке (для одного продукта):

- масляная (бутановая) кислота C4:0, %

- капроновая (гексановая) кислота C6:0, %

- каприловая (октановая) кислота C8:0, %

- каприновая (декановая) кислота C10:0, %

- ундециловая (ундекановая) кислота C11:0, %

- лауриновая (додекановая) кислота C12:0, %

- тридециловая (тридекановая) кислота C13:0, %

- миристиновая (тетрадекановая) кислота C14:0, %

- пентадециловая (пентадекановая) кислота C15:0, %

- пальмитиновая (гексадекановая) кислота C16:0, %

- маргариновая (гептадекановая) кислота C17:0, %

- стеариновая (октадекановая) кислота C18:0, %

- арахиновая (эйкозановая) кислота C20:0, %

- генэйкоциловая (генэйкозановая) кислота C21:0, %

- бегеновая (докозановая) кислота C22:0, %

- лигноцериновая (тетракозановая) кислота C24:0, %

- миристолеиновая (цис-9-тетрадеценовая) кислота C14:1, %

- пентадеценовая кислота C15:1, %

- пальмитолеиновая (цис-9-гексадеценовая) кислота C16:1, %

- маргаринолеиновая (гептадеценовая) кислота C17:1, %

- олеиновая (цис-9-октадеценовая) кислота C18:1, %

- элаидиновая (транс-9-октадеценовая) кислота C18:1, %

- эйкозеновая (гондоиновая) кислота C20:1, %

- эруковая (цис-13-докозеновая) кислота C22:1, %

- нервоновая (селахолевая) кислота C24:1, %

- линолевая (цис, цис-9, 12-октадекадиеновая) кислота C18:2, %

- линоэладиковая кислота C18:2, %

- альфа-линоленовая (цис, цис, цис-9, 12, 15-октадекатриеновая) кислота C18:3, %

- гамма-линоленовая (цис, цис, цис-6, 9, 12-октадекатриеновая) кислота C18:3, %

- эйкозадиеновая (эйкозадиеновая) кислота C20:2, %

- эйкозатриеновая (цис, цис, цис-8, 11, 14-эйкозатриеновая) кислота C20:3n6, %

- эйкозатриеновая (цис, цис, цис-11, 14, 17-эйкозатриеновая) кислота C20:3n3, %

- арахидоновая (цис-5, 8, 11, 14-эйкозотетраеновая) кислота C20:4, %

- эйкозапентаеновая (тимнодоновая) кислота C20:5, %

- докозадиеновая (цис, цис-13, 16-докозадиеновая) кислота C22:2, %

- цервоновая (докозагексаеновая) кислота C22:6, %

- адреновая (докозатетраеновая) кислота C22:4, %

- клупанодоновая (докозапентаеновая) кислота C22:5, %

Полученное значение записывается во вновь созданный столбец "Оценка качества исследования ЖКС". Те образцы, которые оказались вне эталонного диапазона для данного показателя , должны быть помечены любым способом и отправлены оператору ввода данных на доработку.