Содержание антигена гемагглютинина в двух вакцинах против гриппа определяли методом радиальной иммунодиффузии. На этикетках обеих вакцин была указана активность 15 мкг гемагглютинина на одну дозу, что соответствует содержанию 30 мкг гемагглютинина/мл. Стандартный образец имел установленную активность 39 мкг гемагглютинина/мл.
Исследовали 4 концентрации стандартного образца и испытуемого препарата, рассчитанные, исходя из ожидаемых и обозначенных на этикетке значений биологической активности; в каждом случае число повторностей равно 2. Контрольную группу не использовали. После установления равновесия между внутренним и внешним реагентом, измеряли площадь кольцевых зон осадка. Результаты приведены в таблице 3.2.8.-26.
Таблица 3.2.8.-26. - Площадь кольцевых зон осадка (определение биологической активности вакцины против гриппа, модель угловых коэффициентов)
PS = S1 + S2 + S3 + S4 = 108,2;
PU = U1 + U2 + U3 + U4 = 103,85;
LS = 1S1 + 2S2 + 3S3 + 4S4 = 301,1;
LU = 1U1 + 2U2 + 2U3 + 4U4 = 292,1;
aS = (4d + 2)PS - 6LS = 141,0;
aU = (4d + 2)PU - 6LU = 116,7;
aU' = (4d + 2)PU' - 6LU' = 139,8.
bU' = 2LU' - (d + 1)PU' = 39,2.
GU' = U1 + U2 + U4 + U5 = 1917,3.
Для того чтобы проверить статистическую значимость источников вариации, пригодность результатов и вычислить дисперсию опыта, проводят дисперсионный анализ полученных данных. При этом рассчитывают значения дисперсий для 6 источников (таблица 3.2.8.-27).
Таблица 3.2.8.-27. - Сводная таблица дисперсионного анализа (определение биологической активности вакцины против гриппа, модель угловых коэффициентов)
|
Наблюдаемое значение критерия Фишера Fнабл. |
Критическое значение критерия Фишера Fкритич. |
||||
|
(p = 0,01) |
|||||
|
(p = 0,05) |
|||||
|
(p = 0,05) |
|||||
Нелинейность = n(JS + JU + JU') = 5,090;
Регрессия = постановки - точка пересечения - нелинейность =
= 1096,2 - 3,474 - 5,090 = 1087,6;
Отклонение = итог - постановки = 1109,0 - 1096,2 - 12,8.
Значимость различий дисперсий проверяют с помощью критерия Фишера. Обязательным является выполнение требований для показателей Регрессия, Точка пересечения и Нелинейность. Эти требования заключаются в том, что для Регрессии наблюдаемое значение критерия Фишера должно быть больше критического (p = 0,01), а для Точки пересечения и Нелинейности - меньше критического (p = 0,05).
Для того чтобы найти Fнабл., средние квадраты показателей делят на средний квадрат показателя Отклонение. Полученные результаты сравнивают с табличными критическими значениями критерия Фишера (таблица 3 Приложения). Число степеней свободы f1 = 3, 2 и 6 соответственно, а f2 = 36.
Дисперсионный анализ показал пригодность результатов опыта.
Вычисление биологической активности и ее доверительных границ
t = 2,179 при f = 12 и p = 0,05;
Угловой коэффициент стандартного образца ![]()
Угловой коэффициент испытуемого образца ![]()
Угловой коэффициент испытуемого образца ![]()
Коэффициенты дисперсии для вычисления доверительных границ
K' = (C - 1)V2 = 0,0056 · 0,625 = 0,0035
Доверительные границы биологической активности испытуемого образца вычисляют по формуле:
Содержание гемагглютинина в 1 мл вакцины находят путем умножения отношения активностей и доверительных интервалов на ожидаемую активность 30 мкг/мл. Результаты приведены в таблице 3.2.8.-28.
Таблица 3.2.8.-28. - Полученное содержание гемагглютинина в вакцинах (мкг/дозу)
Примечание. При использовании контрольной группы (схема "(hd) + 1") имеют место следующие отличия.
2) В сводной таблице дисперсионного анализа появляется дополнительный источник вариации: Контроль (после Регрессии).
Контроль = HB (B - a)2 при f = 1.
3) Постановки = n(B2 + GS + GU +...) - K при f = hd.
4) Регрессия = постановки - контроль - точка пересечения - нелинейность.
7) Число степеней свободы для показателя Отклонение равно (hd + 1)(n - 1).
8) Число степеней свободы для показателя Итог равно nhd + n - 1.
Вычисление биологической активности и ее доверительных границ
- Гражданский кодекс (ГК РФ)
- Жилищный кодекс (ЖК РФ)
- Налоговый кодекс (НК РФ)
- Трудовой кодекс (ТК РФ)
- Уголовный кодекс (УК РФ)
- Бюджетный кодекс (БК РФ)
- Арбитражный процессуальный кодекс
- Конституция РФ
- Земельный кодекс (ЗК РФ)
- Лесной кодекс (ЛК РФ)
- Семейный кодекс (СК РФ)
- Уголовно-исполнительный кодекс
- Уголовно-процессуальный кодекс
- Производственный календарь на 2025 год
- МРОТ 2026
- ФЗ «О банкротстве»
- О защите прав потребителей (ЗОЗПП)
- Об исполнительном производстве
- О персональных данных
- О налогах на имущество физических лиц
- О средствах массовой информации
- Производственный календарь на 2026 год
- Федеральный закон "О полиции" N 3-ФЗ
- Расходы организации ПБУ 10/99
- Минимальный размер оплаты труда (МРОТ)
- Календарь бухгалтера на 2026 год
- Частичная мобилизация: обзор новостей
- Постановление Правительства РФ N 1875
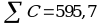
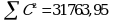
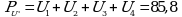 .
.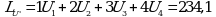 .
.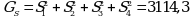 ;
;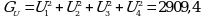 ;
;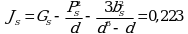 ;
;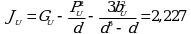 ;
;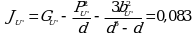 ;
;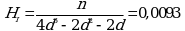 ;
;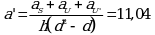 ;
;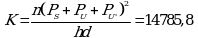 .
.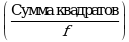
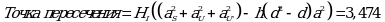 ;
;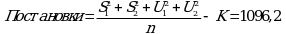 ;
;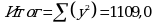 ;
;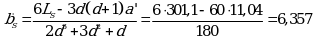 .
.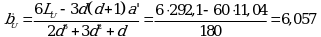 .
.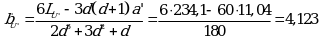 .
.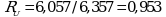 ;
;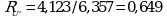 .
.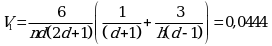 ;
;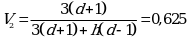 ;
;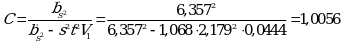
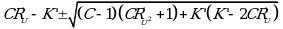 .
.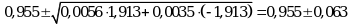 .
.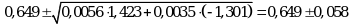 .
.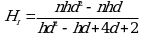
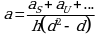 .
.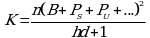 .
.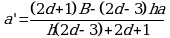 .
.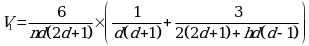 .
. .
.