В большинстве случаев среднее значение выборки ![]() является наилучшей оценкой истинного значения измеряемой величины
является наилучшей оценкой истинного значения измеряемой величины ![]() , если его вычисляют как среднее арифметическое всех вариант:
, если его вычисляют как среднее арифметическое всех вариант:
При этом разброс вариант xi вокруг среднего значения ![]() характеризуется величиной стандартного отклонения s. При количественном определении веществ методами физического, физико-химического и химического анализа величину s часто рассматривают как меру случайной погрешности, свойственной данной методике анализа. Квадрат этой величины s2 называют дисперсией. Величина дисперсии может рассматриваться как мера прецизионности (сходимости) результатов, представленных в данной выборке. Вычисление величин s и s2 проводят по уравнениям (1.5) и (1.6). Иногда для этого предварительно определяют значения отклонений di и число степеней свободы (число независимых вариант) f:
характеризуется величиной стандартного отклонения s. При количественном определении веществ методами физического, физико-химического и химического анализа величину s часто рассматривают как меру случайной погрешности, свойственной данной методике анализа. Квадрат этой величины s2 называют дисперсией. Величина дисперсии может рассматриваться как мера прецизионности (сходимости) результатов, представленных в данной выборке. Вычисление величин s и s2 проводят по уравнениям (1.5) и (1.6). Иногда для этого предварительно определяют значения отклонений di и число степеней свободы (число независимых вариант) f:
Стандартное отклонение среднего результата ![]() рассчитывают по уравнению:
рассчитывают по уравнению:
При обработке результатов испытаний лекарственных средств во многих случаях целесообразно использовать относительные (по отношению к ![]() ) величины, например, относительное стандартное отклонение sr относительную дисперсию
) величины, например, относительное стандартное отклонение sr относительную дисперсию ![]() и относительное стандартное отклонение среднего результата
и относительное стандартное отклонение среднего результата ![]() . Их рассчитывают по формулам:
. Их рассчитывают по формулам:
Указанные относительные величины в зависимости от решаемой задачи могут выражаться в процентах относительно ![]() . В этом случае их часто обозначают RSD и
. В этом случае их часто обозначают RSD и  , соответственно:
, соответственно:
Относительное стандартное отклонение среднего результата, выраженное в процентах  называют коэффициентом вариации. При обработке результатов испытаний лекарственных средств абсолютные величины обычно используют для прямых, а относительные - для косвенных методов анализа.
называют коэффициентом вариации. При обработке результатов испытаний лекарственных средств абсолютные величины обычно используют для прямых, а относительные - для косвенных методов анализа.
Если при измерениях получают логарифмы искомых вариант, среднее значение выборки вычисляют как среднее геометрическое, используя логарифм вариант:
Значения s2, s и ![]() в этом случае также рассчитывают, исходя из логарифмов вариант, и обозначают соответственно через
в этом случае также рассчитывают, исходя из логарифмов вариант, и обозначают соответственно через ![]() , slg,
, slg, ![]() .
.
Пример вычисления среднего значения и дисперсии приведен в разделе 6.1.
- Гражданский кодекс (ГК РФ)
- Жилищный кодекс (ЖК РФ)
- Налоговый кодекс (НК РФ)
- Трудовой кодекс (ТК РФ)
- Уголовный кодекс (УК РФ)
- Бюджетный кодекс (БК РФ)
- Арбитражный процессуальный кодекс
- Конституция РФ
- Земельный кодекс (ЗК РФ)
- Лесной кодекс (ЛК РФ)
- Семейный кодекс (СК РФ)
- Уголовно-исполнительный кодекс
- Уголовно-процессуальный кодекс
- Производственный календарь на 2025 год
- МРОТ 2026
- ФЗ «О банкротстве»
- О защите прав потребителей (ЗОЗПП)
- Об исполнительном производстве
- О персональных данных
- О налогах на имущество физических лиц
- О средствах массовой информации
- Производственный календарь на 2026 год
- Федеральный закон "О полиции" N 3-ФЗ
- Расходы организации ПБУ 10/99
- Минимальный размер оплаты труда (МРОТ)
- Календарь бухгалтера на 2026 год
- Частичная мобилизация: обзор новостей
- Постановление Правительства РФ N 1875
 . (1.2)
. (1.2) , (1.3)
, (1.3) , (1.5)
, (1.5) . (1.6)
. (1.6)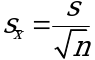 . (1.7)
. (1.7) , (1.5а)
, (1.5а) , (1.6а)
, (1.6а) . (1.7а)
. (1.7а) . (1.7б)
. (1.7б) . (1.8),
. (1.8),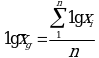 , (1.9)
, (1.9)