Общий случай. Рассчитывают неопределенности конечной аналитической операции 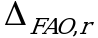 для испытуемого раствора и раствора сравнения. При расчете доверительных интервалов используют односторонний коэффициент Стьюдента для вероятности 95% (равен 90% для двустороннего распределения), который для числа степени свободы (5 - 1 = 4) равен 2,13. Доверительные интервалы рассчитывают для среднего из 5 результатов, поэтому в знаменателе ставим
для испытуемого раствора и раствора сравнения. При расчете доверительных интервалов используют односторонний коэффициент Стьюдента для вероятности 95% (равен 90% для двустороннего распределения), который для числа степени свободы (5 - 1 = 4) равен 2,13. Доверительные интервалы рассчитывают для среднего из 5 результатов, поэтому в знаменателе ставим ![]() :
:
Суммарная неопределенность конечной аналитической операции:
Используя уравнение (5.7), рассчитывают суммарную неопределенность анализа ![]() :
:
Использование объединенного стандартного отклонения.
Суммарную неопределенность анализа можно уменьшить за счет использования объединенного стандартного отклонения для конечной аналитической операции. Для этого нужно учесть, что RSD и RSDst являются выборочными величинами одной и той же генеральной совокупности. Проверяют вначале по Фишеру гипотезу о равенстве дисперсий:
Как видно, расчетное значение отношения дисперсий гораздо ниже табличного значения F-критерия на 95% уровне значимости. Поэтому можно принять гипотезу о равенстве дисперсий и принять формулы подраздела 1.4. настоящей общей фармакопейной статьи для объединения выборок.
Рассчитывают объединенное стандартное отклонение по уравнению:
RSDtot имеет число степеней свободы 2 - (5 - 1) = 8. Коэффициент Стьюдента для данного числа степеней свободы и односторонней вероятности 0,95 равен 1,86. Тогда доверительные интервалы результатов конечной аналитической операции для испытуемого и стандартного растворов будут равны:
Суммарная неопределенность конечной аналитической операции равна:
Используя уравнение (5.7) рассчитывают суммарную неопределенность анализа ![]() :
:
Как видно, данная величина меньше величины, полученной для обычного случая (1,29%).
- Гражданский кодекс (ГК РФ)
- Жилищный кодекс (ЖК РФ)
- Налоговый кодекс (НК РФ)
- Трудовой кодекс (ТК РФ)
- Уголовный кодекс (УК РФ)
- Бюджетный кодекс (БК РФ)
- Арбитражный процессуальный кодекс
- Конституция РФ
- Земельный кодекс (ЗК РФ)
- Лесной кодекс (ЛК РФ)
- Семейный кодекс (СК РФ)
- Уголовно-исполнительный кодекс
- Уголовно-процессуальный кодекс
- Производственный календарь на 2025 год
- МРОТ 2026
- ФЗ «О банкротстве»
- О защите прав потребителей (ЗОЗПП)
- Об исполнительном производстве
- О персональных данных
- О налогах на имущество физических лиц
- О средствах массовой информации
- Производственный календарь на 2026 год
- Федеральный закон "О полиции" N 3-ФЗ
- Расходы организации ПБУ 10/99
- Минимальный размер оплаты труда (МРОТ)
- Календарь бухгалтера на 2026 год
- Частичная мобилизация: обзор новостей
- Постановление Правительства РФ N 1875
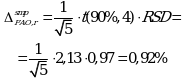 .
.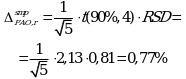 .
.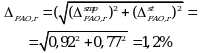 .
.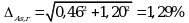 .
.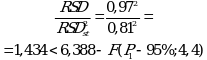 .
.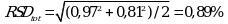 .
.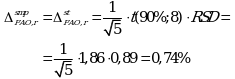 .
.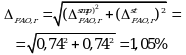 .
.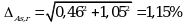 .
.