Если случайная однородная выборка конечного объема n получена в результате последовательных измерений некоторой величины A, имеющей истинное значение ![]() , то среднее этой выборки
, то среднее этой выборки ![]() следует рассматривать лишь как приближенную оценку величины A. Достоверность этой оценки характеризуется величиной доверительного интервала
следует рассматривать лишь как приближенную оценку величины A. Достоверность этой оценки характеризуется величиной доверительного интервала 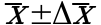 , для которой с заданной доверительной вероятностью P выполняется условие:
, для которой с заданной доверительной вероятностью P выполняется условие:
Данный доверительный интервал не характеризует погрешность определения величины ![]() , поскольку найденная величина
, поскольку найденная величина ![]() может быть в действительности очень близка к истинному значению
может быть в действительности очень близка к истинному значению ![]() , которое остается неизвестным. Полученный доверительный интервал характеризует степень неопределенности наших знаний об истинном значении
, которое остается неизвестным. Полученный доверительный интервал характеризует степень неопределенности наших знаний об истинном значении ![]() величины A по результатам последовательных измерений выборки конечного объема n. Поэтому правильно говорить о "неопределенности результатов анализа", которая характеризуется доверительным интервалом, вместо выражения "погрешность результатов анализа", которое нередко не совсем корректно используется.
величины A по результатам последовательных измерений выборки конечного объема n. Поэтому правильно говорить о "неопределенности результатов анализа", которая характеризуется доверительным интервалом, вместо выражения "погрешность результатов анализа", которое нередко не совсем корректно используется.
Расчет граничных значений доверительного интервала при известном значении стандартного отклонения s или для выборок большого объема проводят по уравнению:
предполагая, что варианты, входящие в выборку, распределены нормально. Здесь U(P) - табличное значение функции нормального распределения.
Для выборок небольшого объема расчет граничных значений доверительного интервала проводят с использованием критерия Стьюдента, предполагая, что варианты, входящие в выборку, распределены нормально:
или с использованием относительных величин:
Здесь t(P, f) - табличное значение критерия Стьюдента (таблица 2 Приложения).
Распределение по критерию Стьюдента t(P, f) является обобщением нормального распределения U(P) и переходит в него при достаточно большом числе степеней свободы f, т.е. t(P, f) ![]() U(P). С учетом этого далее для единообразия везде используется более часто употребляемые соотношения (1.22б) и (1.22в), даже в случае выборок достаточно большого объема.
U(P). С учетом этого далее для единообразия везде используется более часто употребляемые соотношения (1.22б) и (1.22в), даже в случае выборок достаточно большого объема.
Полуширины относительных доверительных интервалов единичного 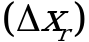 и среднего
и среднего 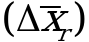 результатов часто выражают в процентах по отношению к
результатов часто выражают в процентах по отношению к ![]() . В этом случае в выражении (1.22в) вместо величины sr используют RSD, а вместо 1 указывают 100%, т.е.:
. В этом случае в выражении (1.22в) вместо величины sr используют RSD, а вместо 1 указывают 100%, т.е.:
Если при измерении одной и той же методикой двух близких значений A были получены две случайные однородные выборки с объемами n и m, то при m < n для выборки объема m справедливо уравнение:
где индекс указывает принадлежность величин к выборке объема m или n.
Уравнение (1.23) позволяет оценить величину доверительного интервала среднего ![]() , найденного, исходя из выборки объема m. Иными словами, доверительный интервал среднего
, найденного, исходя из выборки объема m. Иными словами, доверительный интервал среднего ![]() для выборки относительно малого объема m может быть сужен благодаря использованию известных величин s(n) и t(P, fn), найденных ранее для выборки большего объема n. Более общим подходом является объединение выборок с расчетом объединенного стандартного отклонения и степеней свободы по уравнениям (1.14) - (1.15). Это стандартное отклонение и соответствующий объединенному числу степеней свободы критерий Стьюдента подставляют затем в выражение (1.22г).
для выборки относительно малого объема m может быть сужен благодаря использованию известных величин s(n) и t(P, fn), найденных ранее для выборки большего объема n. Более общим подходом является объединение выборок с расчетом объединенного стандартного отклонения и степеней свободы по уравнениям (1.14) - (1.15). Это стандартное отклонение и соответствующий объединенному числу степеней свободы критерий Стьюдента подставляют затем в выражение (1.22г).
Аналогично уравнениям (1.21) - (1.22) определяют доверительный интервал результата отдельного определения. Подставляя n = 1 в уравнение (1.22б) или m = 1 в уравнение (1.23), получают:
или с использованием относительных величин:
Этот интервал является доверительным интервалом результата отдельного определения. Для него с доверительной вероятностью P выполняются взаимосвязанные условия:
Значения ![]() и
и ![]() из уравнений (1.22б) и (1.24) используют при вычислении относительных неопределенностей отдельной варианты
из уравнений (1.22б) и (1.24) используют при вычислении относительных неопределенностей отдельной варианты ![]() и среднего результата
и среднего результата ![]() , выражая эти величины в процентах:
, выражая эти величины в процентах:
Пример расчета доверительных интервалов в процентах и относительных неопределенностей приведен в разделе 6.3.
Если при измерениях получают логарифмы исходных вариант, то уравнения (1.22б) и (1.24) принимают вид:
Потенцирование выражений (1.29) и (1.30) приводит к несимметричным доверительным интервалам для значений ![]() и xi:
и xi:
При этом для нижних и верхних границ доверительных интервалов ![]() и x относительные неопределенности составляют:
и x относительные неопределенности составляют:
- Гражданский кодекс (ГК РФ)
- Жилищный кодекс (ЖК РФ)
- Налоговый кодекс (НК РФ)
- Трудовой кодекс (ТК РФ)
- Уголовный кодекс (УК РФ)
- Бюджетный кодекс (БК РФ)
- Арбитражный процессуальный кодекс
- Конституция РФ
- Земельный кодекс (ЗК РФ)
- Лесной кодекс (ЛК РФ)
- Семейный кодекс (СК РФ)
- Уголовно-исполнительный кодекс
- Уголовно-процессуальный кодекс
- Производственный календарь на 2025 год
- МРОТ 2026
- ФЗ «О банкротстве»
- О защите прав потребителей (ЗОЗПП)
- Об исполнительном производстве
- О персональных данных
- О налогах на имущество физических лиц
- О средствах массовой информации
- Производственный календарь на 2026 год
- Федеральный закон "О полиции" N 3-ФЗ
- Расходы организации ПБУ 10/99
- Минимальный размер оплаты труда (МРОТ)
- Календарь бухгалтера на 2026 год
- Частичная мобилизация: обзор новостей
- Постановление Правительства РФ N 1875
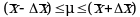 . (1.21)
. (1.21)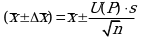 , (1.22а)
, (1.22а)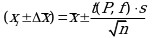 (1.22б)
(1.22б)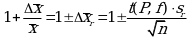 . (1.22в)
. (1.22в)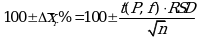 . (1.22г)
. (1.22г)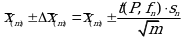 , (1.23)
, (1.23)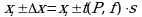 (1.24)
(1.24)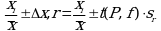 . (1.24а)
. (1.24а)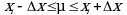 , (1.25)
, (1.25)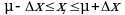 . (1.26)
. (1.26)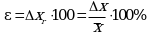 , (1.27)
, (1.27)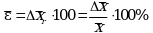 . (1.28)
. (1.28)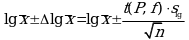 ; (1.29)
; (1.29)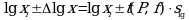 . (1.30)
. (1.30)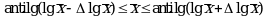 ; (1.31)
; (1.31)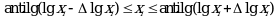 , (1.32)
, (1.32)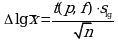 , (1.33)
, (1.33)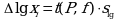 . (1.34)
. (1.34)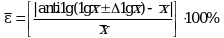 , (1.35а)
, (1.35а)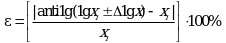 . (1.35б).
. (1.35б).