Если в результате измерений одной и той же величины A получены две выборки объема n1 и n2, причем 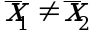 , может возникнуть необходимость проверки статистической достоверности гипотезы:
, может возникнуть необходимость проверки статистической достоверности гипотезы:
т.е. значимости величины разности 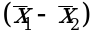 .
.
Такая проверка необходима, например, если величина A определялась двумя разными методиками с целью их сравнения, или, если величина A определялась одной и той же методикой для двух разных объектов, идентичность которых требуется доказать. Для проверки гипотезы (3.3) следует установить, существует ли статистически значимое различие между дисперсиями ![]() и
и ![]() . Эта проверка проводится так же, как при сравнении двух методик анализа по воспроизводимости согласно уравнениям (2.1) - (2.3).
. Эта проверка проводится так же, как при сравнении двух методик анализа по воспроизводимости согласно уравнениям (2.1) - (2.3).
Различие дисперсий ![]() и
и ![]() статистически незначимо, когда справедливо неравенство (2.3). В этом случае средневзвешенное значение s2, учитывающее не только количество выборок (дисперсий), но и их объем, вычисляют по уравнению (1.5), а дисперсию
статистически незначимо, когда справедливо неравенство (2.3). В этом случае средневзвешенное значение s2, учитывающее не только количество выборок (дисперсий), но и их объем, вычисляют по уравнению (1.5), а дисперсию ![]() разности
разности 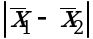 - по уравнению:
- по уравнению:
Далее вычисляют критерий Стьюдента:
Если при выбранном значении P2 (например, при P2 = 95%):
то результат проверки положителен: разность 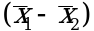 является значимой и гипотезу
является значимой и гипотезу 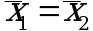 отбрасывают. В противном случае надо признать, что эта гипотеза не противоречит экспериментальным данным.
отбрасывают. В противном случае надо признать, что эта гипотеза не противоречит экспериментальным данным.
Различие дисперсий ![]() и
и ![]() статистически значимо, когда справедливо неравенство (2.2). Если
статистически значимо, когда справедливо неравенство (2.2). Если 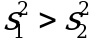 , дисперсию
, дисперсию ![]() разности
разности 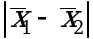 находят по уравнению (3.7), а число степеней свободы f' - по уравнению (3.8):
находят по уравнению (3.7), а число степеней свободы f' - по уравнению (3.8):
Следовательно, в данном случае:
Вычисленное по уравнению (3.9) значение t сравнивают с табличным значением t(P2, f'), как это описано выше для первого случая.
Приведенные выше расчеты упрощаются, когда 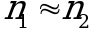 и
и 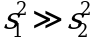 . Тогда в отсутствие систематической погрешности среднее
. Тогда в отсутствие систематической погрешности среднее ![]() выборки объема n2 принимают за достаточно точную оценку величины A, т.е. принимают
выборки объема n2 принимают за достаточно точную оценку величины A, т.е. принимают 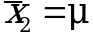 . Справедливость гипотезы
. Справедливость гипотезы 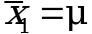 , эквивалентной гипотезе (3.3), проверяют с помощью уравнений (1.38) и (1.39), принимая f1 = n1 - 1. Гипотеза (3.3) отклоняется как статистически недостоверная, если выполнятся неравенство (1.39).
, эквивалентной гипотезе (3.3), проверяют с помощью уравнений (1.38) и (1.39), принимая f1 = n1 - 1. Гипотеза (3.3) отклоняется как статистически недостоверная, если выполнятся неравенство (1.39).
Известно точное значение величины A. Если 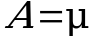 , проверяют две гипотезы:
, проверяют две гипотезы: 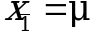 и
и 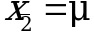 . Проверку выполняют с помощью уравнений (1.38) и (1.39) отдельно для каждой из гипотез. Если обе проверяемые гипотезы статистически достоверны, то следует признать достоверной и гипотезу (3.3). В противном случае гипотеза (3.3) должна быть отброшена.
. Проверку выполняют с помощью уравнений (1.38) и (1.39) отдельно для каждой из гипотез. Если обе проверяемые гипотезы статистически достоверны, то следует признать достоверной и гипотезу (3.3). В противном случае гипотеза (3.3) должна быть отброшена.
Если при измерениях получают логарифмы исходных вариант, при сравнении средних используют величины ![]() ,
, ![]() и slg. В тех случаях, когда разность
и slg. В тех случаях, когда разность 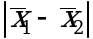 оказывается значимой, определяют доверительный интервал для разности соответствующих генеральных средних
оказывается значимой, определяют доверительный интервал для разности соответствующих генеральных средних ![]() и
и ![]() :
:
Пример сравнения средних результатов двух выборок приведен в разделе 6.5.
- Гражданский кодекс (ГК РФ)
- Жилищный кодекс (ЖК РФ)
- Налоговый кодекс (НК РФ)
- Трудовой кодекс (ТК РФ)
- Уголовный кодекс (УК РФ)
- Бюджетный кодекс (БК РФ)
- Арбитражный процессуальный кодекс
- Конституция РФ
- Земельный кодекс (ЗК РФ)
- Лесной кодекс (ЛК РФ)
- Семейный кодекс (СК РФ)
- Уголовно-исполнительный кодекс
- Уголовно-процессуальный кодекс
- Производственный календарь на 2025 год
- МРОТ 2026
- ФЗ «О банкротстве»
- О защите прав потребителей (ЗОЗПП)
- Об исполнительном производстве
- О персональных данных
- О налогах на имущество физических лиц
- О средствах массовой информации
- Производственный календарь на 2026 год
- Федеральный закон "О полиции" N 3-ФЗ
- Расходы организации ПБУ 10/99
- Минимальный размер оплаты труда (МРОТ)
- Календарь бухгалтера на 2025 год
- Частичная мобилизация: обзор новостей
- Постановление Правительства РФ N 1875
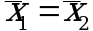 , (3.3)
, (3.3)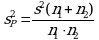 , (3.4)
, (3.4)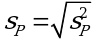 . (3.4а)
. (3.4а)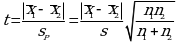 , (3.5)
, (3.5)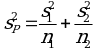 ; (3.7)
; (3.7)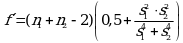 . (3.8)
. (3.8)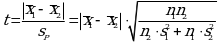 . (3.9)
. (3.9) . (3.10)
. (3.10)