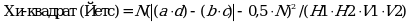2.3. Оценка достоверности полученной информации
Достоверность (validity) - характеристика, показывающая, в какой мере полученный результат соответствует истинной величине. Достоверность исследования определяется тем, в какой мере полученные результаты справедливы в отношении данной выборки (internal validity). Это характеристика, касаемая именно данной исследуемой группы, не обязательно распространяется на другие группы.
Достоверность полученных результатов в аналитических исследованиях оценивают при помощи значения p, доверительного интервала (CI) и значения Хи-квадрат. Значение p - статистический показатель, позволяющий оценить, в каких пределах может находиться истинное значение параметра в популяции; диапазон колебаний истинных значений. Величины, полученные в исследованиях на выборке, отличаются от истинных величин в популяции вследствие влияния случайности. Так, 95%-й доверительный интервал означает, что истинное значение величины с вероятностью в 95% лежит в его пределах. В эпидемиологических исследованиях значение p должно быть не более 0,05. Доверительный интервал (CI) - диапазон колебаний истинных значений.
Тесты Хи-квадрат и соответствующие им значения p указывают, насколько вероятно (или невероятно) то, что наблюдаемая ассоциация (связь) изучаемого фактора риска и заболеваемости была случайна. Чем больше значение Хи-квадрата, тем меньше соответствующее значение p. На статистическую значимость оказывает влияние как сила ассоциации (например, высокое отношение рисков или шансов), так и количество субъектов в исследовании. Нельзя использовать тесты Хи-квадрат, если ожидаемое значение в любой из четырех клеток таблицы 2 x 2 менее 5. Вместо этого необходимо использовать точный тест Фишера.
Ниже приводятся три значения Хи-квадрата, полученные с помощью различных методов: нескорректированной формулы (без поправки), формулы Мантель-Гензеля и Йетса; далее приводятся соответствующие значения p. Используемые формулы выглядят следующим образом:
где N = a + b + c + d, H1 = a + b, H2 = c + d, V1 = a + c, V2 = b + d.
Данную формулу не рекомендуется использовать для таблиц, в которых N меньше 30.
Формула для вычисления Хи-квадрата, скорректированная по Йетсу, приводит к самому маленькому значению Хи-квадрата из всех трех формул и, следовательно, к самому высокому значению p. Соответственно, она называется самой консервативной из этих трех формул.
- Гражданский кодекс (ГК РФ)
- Жилищный кодекс (ЖК РФ)
- Налоговый кодекс (НК РФ)
- Трудовой кодекс (ТК РФ)
- Уголовный кодекс (УК РФ)
- Бюджетный кодекс (БК РФ)
- Арбитражный процессуальный кодекс
- Конституция РФ
- Земельный кодекс (ЗК РФ)
- Лесной кодекс (ЛК РФ)
- Семейный кодекс (СК РФ)
- Уголовно-исполнительный кодекс
- Уголовно-процессуальный кодекс
- Производственный календарь на 2025 год
- МРОТ 2026
- ФЗ «О банкротстве»
- О защите прав потребителей (ЗОЗПП)
- Об исполнительном производстве
- О персональных данных
- О налогах на имущество физических лиц
- О средствах массовой информации
- Производственный календарь на 2026 год
- Федеральный закон "О полиции" N 3-ФЗ
- Расходы организации ПБУ 10/99
- Минимальный размер оплаты труда (МРОТ)
- Календарь бухгалтера на 2025 год
- Частичная мобилизация: обзор новостей
- Постановление Правительства РФ N 1875
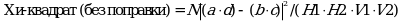 ,
,