VI. Полезность и конфиденциальность. Показатели потери информации
VI. Полезность и конфиденциальность. Показатели
потери информации
Все методы защиты информации неизбежно ведут к снижению информационного содержания файла микроданных. При выборе оптимальных методов и решений для деперсонификации микроданных необходимо стремиться к минимизации риска раскрытия, обеспечивая при этом максимальную полезность статистических данных с позиции их последующего анализа.
Общий показатель потери информации оценивает объем потерянной информации применительно к разумному спектру способов использования данных. Потеря информации была небольшой, если массив защищенных данных является аналитически адекватным и интересным, в соответствии со следующими определениями:
массив защищенных микроданных является аналитически адекватным, если следующие его характеристики примерно соответствуют оригинальным данным: средние значения и ковариации для отдельных подмножеств записей и/или переменных; характеристики распределения
массив микроданных является аналитически интересным, если в нем представлены как минимум шесть переменных, пригодных для корректного анализа.
Оценка потери информации для численных переменных выполняется с использованием следующих описательных статистик, рассчитанных для оригинального и модифицированного (защищенного) массива данных:
форма распределения переменных;
квантили переменных и соотношений переменных.
Сравнение должно быть выполнено для каждой комбинации ключевых категориальных переменных.
Пока нет единого количественного показателя, который полностью отражал бы структурные различия между оригинальными и защищенными данными, поэтому измерять потери информации и, соответственно, безопасность данных предлагается также через различия между матрицей X для исходных данных и соответствующей матрицей X' для защищенного массива данных.
Величину расхождения (ошибки) между матрицами (X - X') можно измерять по крайней мере тремя способами.
среднеквадратическая ошибка: сумма квадратов различий между соответствующими компонентами матриц, деленная на количество ячеек в каждой матрице:
средняя абсолютная ошибка: сумма абсолютных различий между соответствующими компонентами соответствующих матриц, деленная на количество ячеек в каждой матрице:
среднее отклонение: сумма абсолютных процентных отклонений компонент матрицы, рассчитанных для защищенных данных, от компонент матрицы, рассчитанных для исходных данных, деленная на количество ячеек в каждой матрице. Преимущество данного подхода в том, что масштаб изменений переменных не имеет значения:
В вышеприведенных формулах p - количество переменных, n - количество записей, а компоненты матриц представлены соответствующими буквами в нижнем регистре (например, ![]() - компонента матрицы X). Деление на
- компонента матрицы X). Деление на ![]() существенно увеличивает среднее отклонение
существенно увеличивает среднее отклонение 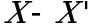 , если исходное значение
, если исходное значение ![]() близко к 0.
близко к 0.
Поскольку такая зависимость от конкретного исходного значения нежелательна для показателя потери информации, предлагается заменить среднее отклонение 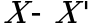 на более стабильный показатель:
на более стабильный показатель:
где ![]() - стандартное отклонение j-й переменной исходного массива данных.
- стандартное отклонение j-й переменной исходного массива данных.
Поскольку необходимо найти приемлемый баланс между потерей информации и риском раскрытия, а последний ограничен - не может быть риска выше 100%, - следует ввести верхнюю границу для показателя потери информации. На практике предлагается ограничить представленные выше показатели, основанные на среднем отклонении, неким заранее выбранным максимальным значением.
- Гражданский кодекс (ГК РФ)
- Жилищный кодекс (ЖК РФ)
- Налоговый кодекс (НК РФ)
- Трудовой кодекс (ТК РФ)
- Уголовный кодекс (УК РФ)
- Бюджетный кодекс (БК РФ)
- Арбитражный процессуальный кодекс
- Конституция РФ
- Земельный кодекс (ЗК РФ)
- Лесной кодекс (ЛК РФ)
- Семейный кодекс (СК РФ)
- Уголовно-исполнительный кодекс
- Уголовно-процессуальный кодекс
- Производственный календарь на 2025 год
- МРОТ 2025
- ФЗ «О банкротстве»
- О защите прав потребителей (ЗОЗПП)
- Об исполнительном производстве
- О персональных данных
- О налогах на имущество физических лиц
- О средствах массовой информации
- Производственный календарь на 2026 год
- Федеральный закон "О полиции" N 3-ФЗ
- Расходы организации ПБУ 10/99
- Минимальный размер оплаты труда (МРОТ)
- Календарь бухгалтера на 2025 год
- Частичная мобилизация: обзор новостей
- Постановление Правительства РФ N 1875
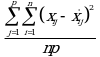
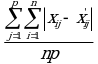
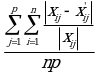
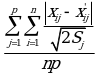 ,
,